Телекоммуникационные технологии.Сети TCP-IP
Пример работы алгоритма SPF
Рассмотрим работу алгоритма на примере базы данных состояния связей рассматриваемой системы.
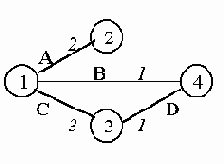
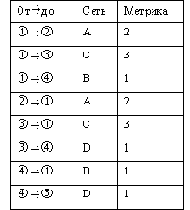
Рис. 5.1.2. OSPF-система и ее база данных состояния связей
Возьмем в качестве вершины S маршрутизатор ?.
Инициализация
S=?
, E={?
}, R={?
,?
,?
}, O={D,C} (из вершины ?
согласно базе данных выходят только связи D (к ?
) и С (к ?
), причем метрика D меньше).
Итерация 1
P=D. Поскольку D ведет от ?
к ?
, то V=?
. Так как V не находится в Е, то кратчайший путь ?
a
?
есть P. Добавляем этот факт в таблицу результатов, изымаем P из O, переносим V из R в Е.
Строим новые пути (шаг 4 алгоритма): согласно базе данных из вершины V=?
существует два односегментных пути: B и D. Добавив их к P=D, получим пути DD и DB с метрикой 2 каждый. Эти пути добавляются в упорядоченный список О.
E={?
,?
}, R={?
,?
}, O={DD,DB,C}.
Результаты: (?
: D)
Итерация 2
P=DD. Двигаясь по этому пути из ?
, мы попадем опять в ?
, то есть V=?
. Так как V находится в Е, то исключаем P из О и переходим к следующей итерации.
E={?
,?
}, R={?
,?
}, O={DB,C}.
Результаты: (?
: D)
Итерация 3
P=DB. Двигаясь по этому пути из ?
, мы попадем в ?
, то есть V=?
. Так как V не находится в Е, то кратчайший путь ?
a
?
есть P. Добавляем этот факт в таблицу результатов, изымаем P из O, переносим V из R в Е.
Строим новые пути: согласно базе данных из V=?
существует три односегментных пути: A,В и C. Добавив их к P=DB, получим пути DBA, DBB и DBC с метриками 4,3 и 5 соответственно. Эти пути добавляются в упорядоченный список О.
E={?
,?
,?
}, R={?
}, O={C, DBB, DBA, DBC}.
Результаты: (?
: D;?
:DB)
Итерация 4
P=С. V=?
. Так как V находится в Е, то исключаем P из О и переходим к следующей итерации.
E={?
,?
,?
}, R={?
}, O={DBB, DBA, DBC}.
Результаты: (?
: D;?
:DB)
Итерация 5
P=DBB. V=?
. Так как V находится в Е, то исключаем P из О и переходим к следующей итерации.
E={?
,?
,?
}, R={?
}, O={DBA, DBC}.
Результаты: (?
: D;?
:DB)
Итерация 6
P=DBA, следовательно V=?
. Так как V не находится в Е, то кратчайший путь ?
